티스토리 뷰
(이 내용은 제가 이해한 걸 정리해둔 거라 틀린 내용이 있을 수도 있습니다.)
(https://www.secmem.org/blog/2019/12/12/HLD/ 를 참고했습니다.)
HLD(Heavy-Light Decomposition) : 트리의 각 노드를 chain 단위로 분할하고 1차원 배열처럼 사용하는 것
트리를 chain단위로 분할하는 과정은
(1) 각 노드들의 무게를 조사한다. 여기서 각 노드의 무게란 자신을 포함한 모든 자식들의 수가 된다.
(2) 루트 노드부터 chain을 형성하게 되는데 자식들 중 가장 무거운 노드들을 chain에 포함하면 시키면서 탐색한다.
(3) 리프노드까지 탐색을 마치면 다시 자신의 부모로 올라가서 탐색을 한다. 2번째부터 탐색되는 노드는 그 노드를 조상으로 하는 새로운 chain을 형성하게 된다.
각 노드에 무게를 조사해서 더 무거운 노드를 chain에 포함시키는 이유는 노드수가 n개인 트리가 있을 때 n/2개인 서브트리는 2개 이상 될 수 없는데 무게가 n/2인 자식이 선택되면 남은 노드수는 n/2 미만이 되므로 계속 절반 이하로 줄어들게 된다. 따라서 HLD가 끝났을 때 최대 log(n)개의 서로 다른 체인이 존재하게 되므로 효율적인 연산을 할 수 있게 된다.
그림으로 보면 더 이해가 잘 돼서 트리를 하나 만들어 예를들어보면

위의 그림처럼 트리가 있을 때 먼저 각 노드들의 무게를 알아봐야 한다.

무게를 알아봤으면 루트 노드를 시작점으로 각 노드들을 chain단위로 분할하면 된다.
분할하는 과정을 자세히 알아보면

1번 노드에서 자식이 2(무게=6), 3(무게=5) 중 더 무거운 2를 chain에 포함하면서 탐색한다.

더 무거운 노드를 chain에 포함시키면서 탐색하면 된다.
4번 노드에서 탐색할 때 8, 9는 무게가 모두 1이므로 아무 곳이나 내려가면 된다.

8번에서는 더 이상 내려갈 곳이 없으므로 다시 부모 노드로 올라가서 탐색한다.

4번 노드에서의 9번은 2번째로 탐색되는 노드이므로 9번 노드를 조상으로 하는 새로운 chain이 생성된다.
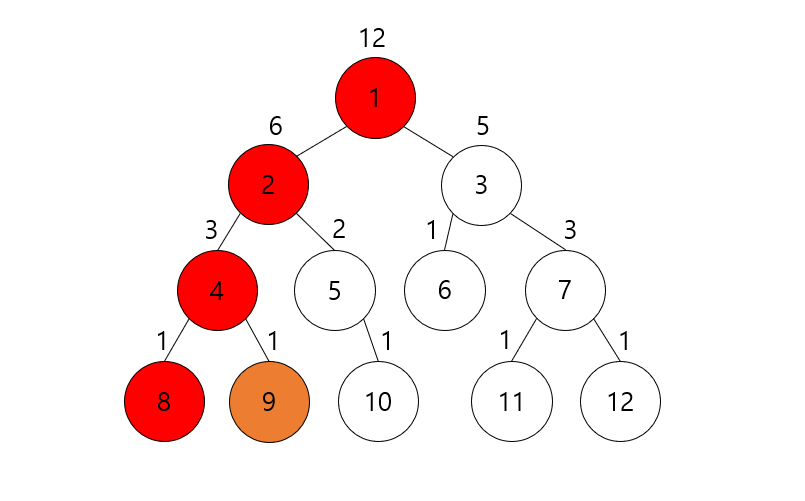
위와 같은 과정을 반복하면 된다. 2번 노드에서도 5번은 2번째로 탐색하는 자식이므로 5를 조상 노드로 하는 새로운 chain(5-10)을 형성하게 되고, 같은 방법으로 3-7-11, 12, 6 도 각 chain을 형성한다.

HLD의 결과는 위의 그림과 같다.
여기서 조상 노드를 chain대푯값이라 하면 1, 2, 4, 8은 1번 chain에 속해있다 할 수 있고, 9는 9번 chain, 5, 10은 5번 이런 식으로 표현 할 수 있다. 이런식으로 표현하면 상위 chain으로 O(1)만에 올라갈 수 있다. 예를 들어 11번 노드에서 1번 노드로 올라가야 한다고 하면 11이 속해있는 3번 chain에서 3을 얻고 3의 부모를 알아보면 바로 올라갈 수 있다.
이를 활용해서 lca를 구할 수 있는데 (lca 말고도 다른 응용분야가 많이 있음) u, v의 lca를 구하는 과정은 다음과 같다.
(1) HLD를 구하는 과정에서 깊이(depth)와 각 노드가 몇 번째로 chain에 저장됐는지(index)를 저장한다. 여기서 깊이는 최초의 chain에서 자신이 속해있는 chain이 얼마나 떨어져 있는가라고 생각하면 된다.
(2) u, v가 같은 chain에 속할 때까지 노드를 계속 올려준다.
(3) u, v가 같은 chain에 속하게 되면 index가 작은 노드가 lca가 된다.
이 과정을 그림으로 보면

먼저 HLD과정에서 깊이를 구해주고

index도 구해준다음(괄호 안의 숫자) 같은 chain에 속할 때까지 올려준다. 여기서 index를 구해주는 이유는 같은 chain에 두 노드가 속했다면 더 작은 index값을 가지는 노드가 lca가 되기 때문이다. 깊이를 저장하는 이유는 두 노드가 다른 chain에 있을 때 어떤 노드를 올려야 할지 알아보기 위함이다. 예를들어 3, 6의 lca를 구하는 과정에서 깊이가 구해져있지않다면 3을 올려야할지 6을 올려야할지 알 수가 없다. 깊이가 깊은 노드를 올려주면 되는데 두 노드의 깊이가 같다면 임의로 하나를 올려준다.
밑의 코드는 BOJ-11438(LCA2)를 HLD로 구현한 내용입니다.
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5;
int sz[N + 2], par[N + 2]; // sz : 노드의 무게, par : 노드의 부모
vector<int> adj[N + 2];
int set_weight(int node, int parent) {
sz[node] = 1;
par[node] = parent;
for (int it : adj[node]) {
if (it == parent) continue;
sz[node] += set_weight(it, node);
}
return sz[node];
}
int depth[N + 2]; // chain의 깊이
int chain_group[N + 2]; // chain의 노드 개수
int chain_num[N + 2]; // 각 노드가 몇 번 chain에 속해있는지
int chain_index[N + 2]; // 각 노드가 chain에서 몇 번째로 저장됐는지
void HLD(int node, int parent, int d, int num) { // d : 깊이, num : 몇 번 chain인지
depth[node] = d;
chain_group[node] = num;
chain_index[node] = ++chain_num[chain_group[num]];
int next = 0;
for (int it : adj[node]) {
if (it != parent && (next == 0 || sz[it] > sz[next])) next = it;
}
if (next) HLD(next, node, d, num); // 기존 chain에 새로운 노드를 포함
for (int it : adj[node]) {
if (chain_group[it] == 0) HLD(it, node, d + 1, it); // 새로운 chain을 생성
}
return;
}
int lca(int a, int b) {
while (chain_group[a] != chain_group[b]) {
if (depth[a] > depth[b]) a = par[chain_group[a]];
else b = par[chain_group[b]];
}
return chain_index[a] > chain_index[b] ? b : a;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n, m;
cin >> n;
for (int u, v; --n;) {
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
set_weight(1, 0);
HLD(1, 0, 0, 1);
cin >> m;
for (int u, v; m--;) {
cin >> u >> v;
cout << lca(u, v) << '\n';
}
return 0;
}
알고리즘의 성능을 알아보기 위해 노드수=5*10^4, 쿼리=10^4인 lca문제를 풀어봤는데

HLD > sparse table > naive 한 방법 순으로 좋았습니다.
'정리' 카테고리의 다른 글
| c++ priority_queue (0) | 2022.01.14 |
|---|---|
| segment tree (0) | 2021.07.12 |
| LCA (0) | 2021.07.01 |
| 그리디 문제 풀기 (0) | 2021.06.25 |
| 이항계수를 어떤수로 나눴을 때 값 구하기 (0) | 2021.06.25 |
