티스토리 뷰
A. Burenka Plays with Fractions
문제 :
정수 $a,b,c,d$가 주어지고 이를 $\frac{a}{b}, \frac{c}{d}$형태로 나타냈을 때 분자 혹은 분모에 $0$이 아닌 특정 값을 곱하는 연산이 있는데 두 값을 같게 하려 할 때 최소 연산 횟수를 구하면 된다.
풀이 :
$ad=bc$이면 답은 $0$이다.
$\frac{a}{b}$의 분자와 분모에 임의의 정수 $x,y$를 곱하면 $\frac{c}{d}$가 된다고 했을 때, $\frac{a}{b}\cdot \frac{x}{y} = \frac{c}{d}$라 하면 $ad\cdot \frac{x}{y}=bc$라고 할 수 있고 $ad\neq0$일때 $\frac{x}{y} = \frac{bc}{ad}$이다. 여기서 $gcd(ad,bc)=ad$이면 $y=1$이라 할 수 있고 이는 $\frac{a}{b}$에 $x$만 곱하면 $\frac{c}{d}$가 된다는 뜻이므로 답은 $1$이다. $\frac{ad}{bc}$인 경우도 같은 방법으로 $gcd(ad,bc)=bc$이면 $1$번의 연산으로 두 값을 같게 할 수 있다.
위의 경우가 모두 아니면 $x>1, y>1$이므로 답은 $2$가 된다.
코드 :
<hide/>
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a % b);
}
void solve() {
ll a, b, c, d;
cin >> a >> b >> c >> d;
if (a * d == b * c) cout << 0;
else if (a * d != 0 && gcd(a * d, b * c) == a * d || b * c != 0 && gcd(a * d, b * c) == b * c) cout << 1;
else cout << 2;
cout << '\n';
return;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int t;
for (cin >> t; t--;) solve();
return 0;
}
B. Interesting Sum
문제 :
길이가 $n$인 수열 $a_1,a_2,...,a_n$과 $1\leq l \leq r \leq n$인 두 정수 $l,r$이 있을 때 $\max(a_1,a_2,...,a_{l-1},a_{r+1},a_{r+2},...a_n) - \min(a_1,a_2,...,a_{l-1},a_{r+1},a_{r+2},...,a_n) + \max(a_l,a_{l+1},...,a_r) - \min(a_l,a_{l+1},...,a_r)$의 값을 구하면 된다.
풀이 :
정렬 후 앞의 두 원소와 마지막 두 원소의 값을 보면 된다.
코드 :
<hide/>
#include<bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> ar(n);
for (int i = 0; i < n; i++) cin >> ar[i];
sort(ar.begin(), ar.end());
int ans = ar.back() - ar.front();
ans += ar[ar.size() - 2] - ar[1];
cout << ans << '\n';
return;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int t;
for (cin >> t; t--;) solve();
return 0;
}
C. Corners
문제 :
$n\times m$크기의 판이 $0,1$로 채워져있다. $2\times 2$크기의 사각형에 $1$이 하나라도 있다면 $1$을 포함하고 $4$칸중 한 칸을 제외한 나머지 값들을 전부 $0$으로 바꾸는 연산이 있다.(ㄱ모양, 회전가능) 모든 칸을 0으로 만들려 할 때 최대 몇 번의 연산을 사용할 수 있는지 구하면 된다.
풀이 :
판에서 $1$이 총 몇개 있는지 개수를 세주고 판에서 특정 형태의 모양이 있는지를 알아본다.
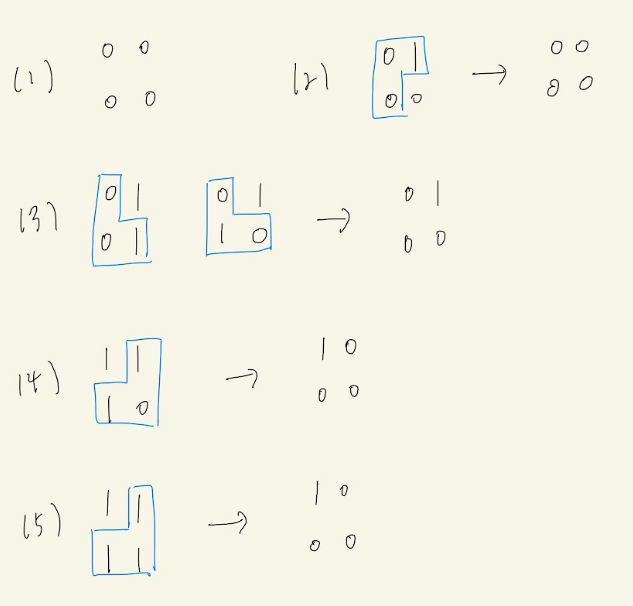
모든 칸이 전부 $1$로 되어 (5)의 모양밖에 없다면 전체 $1$의 개수에서 $2$를 뺀 값이 답이 된다.
(4)의 모양이 있다면 전체 $1$의 개수에서 $1$을 뺀 값이 답이 된다.
나머지 경우는 한 번의 연산에 필요한 $1$의 개수는 $1$개이기 때문에 전체 $1$의 개수가 답이 된다.
코드 :
<hide/>
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
char str[502][502];
void solve() {
int n, m, cnt = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> &str[i][1];
for (int j = 1; j <= m; j++) if (str[i][j] == '1') cnt++;
}
int temp, maxi = 0;
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
temp = 0;
for (int k = 0; k < 2; k++) {
if (str[i][j + k] == '0') temp++;
if (str[i + 1][j + k] == '0') temp++;
}
if (temp > maxi) maxi = temp;
}
}
if (maxi > 1) cout << cnt;
else if (maxi == 1) cout << cnt - 1;
else cout << cnt - 2;
cout << '\n';
return;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int t;
for (cin >> t; t--;) solve();
return 0;
}
D1. Xor-Subsequence (easy version)
D2. Xor-Subsequence (hard version)
문제 :
~~
E. Misha and Paintings
'ps' 카테고리의 다른 글
| educational codeforces round 134 (div.2) (0) | 2022.09.07 |
|---|---|
| codeforces round 816 (div.2) (0) | 2022.09.06 |
| codeforces round 814 (div.2) (0) | 2022.08.25 |
| codeforces round 813 (div.2) (0) | 2022.08.20 |
| codeforces round 812 (div.2) (0) | 2022.08.17 |
